1. 통계 분석의 이해
1. 통계 분석
(1) 통계학 개론: 모집단/표본(sample), 표본 추출방법(4), 자료의 종류(4)
(2) 기초 통계 분석: 기술 통계/추측통계, 회귀분석
(3) 다변량 분석: 상관 분석(상관계수), 다차원 척도법(MDS), 주성분 분석(PCA)
(4) 시계열 예측
2. 통계
- 특정 집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 대한 요약된 형태의 표현
- 통계 자료의 획득 방법: 총조사(census), 표본조사(sampling)
3. 모집단과 표본

4. 표본 추출 방법(4가지, 확률표본 추출)
① 단순랜덤추출법(simple random sampling)
- N개의 원소로 구성된 모집단에서 n개의 표본을 추출할 때 각 원소에 1, 2, 3, ..., N까지의 번호를 부여, n개의 번호를 임의로 선택해 그 번호에 해당하는 원소를 표본 추출(복원/비복원 방법)
② 계통추출법(systematic sampling)
- 모집단의 모든 원소들에게 1, 2, 3, ..., N의 일련번호를 부여하고 이를 순서대로 나열한 후에 K개(K=N/n)씩 n개의 구간으로 나눈다. 첫 구간(1, 2, 3, ..., K)에서 하나의 임의로 선택한 후 K개씩 띄어서 표본을 추출한다.
③ 집락추출법(cluster sampling)
- 모집단이 몇 개의 집락(cluster)이 결합된 형태로 구성돼 있고, 각 집단에서 원소들에게 일련번호를 부여할 수 있는 경우에 이용된다.
- 집락 내부는 이질적, 집락 간에는 동질적 특성
- 일부 집락을 랜덤으로 선택하고 선택된 각 집락에서 표본을 임의로 선택한다.
④ 층화추출법(stratified sampling)
- 상당히 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법.
- 이질적인 모집단의 원소들을 서로 유사한 것끼리 몇 개의 층(stratum)으로 나눈 후, 각 층에서 표본을 랜덤하게 추출한다.
- 집락 내부는 동질적, 집락 간에는 이질적 특성
[기출문제] 조사하고 하는 대상 집단 전체인 모집단 모두를 조사하는 것은 많은 비용과 시간이 소요되므로
모집단을 적절히 대표할 수 있는 일부 원소들을 뽑아 관찰 파악하여 모집단에 대해 유추한다. 이 때 추출한
모집단의 부분집합을 지칭하는 것은 무엇인가?
정답: 표본(sample)
[기출문제] 아래에서 설명하는 표본 추출 방법은 무엇인가? 상당히 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법 이다. 이질적인 모집단의 원소들로 서로 유사한 것끼리 몇 개의 층을 나눈 후, 각 계층에서 표본을 랜덤 하게 추출한다.
정답: 층화추출법
5. 자료의 측정 방법 = 자료의 척도(4가지)
- 명목척도, 순서척도, 구간척도, 비율척도
* 척도 비교
| 질적 자료 이산형 자료 ) |
명목 척도 |
측정대상이 어느 집단에 속하는지 분류할 때 사용되는 척도 (예) 성별(남 , 여), 출생지(서울시, 부산시, 경기도 등), 혈액형, 주소 |
| 순서 척도 |
측정대상 특성이 가지는 서열 관계를 관측하는 척도 , 선택사항이 일정한 순서로 되어 있다 . 특정 서비스의 선호도를 아주 좋아한다, 좋아한다, 그저 그렇다, 싫어한다, 아주 싫어한다로 구분해 묻는 경우에 관측된 자료 (예) 직급, 계급, 순위, 등급, 선호도조사 |
|
| 양적 자료 연속형 자료 |
구간 척도 |
측정대상이 갖고 있는 속성의 양 측정하는 것으로 측정 결과가 숫자로 표현되거나 해당 속성이 전혀 없는 상태인 절대적인 원점 ( 이 없다 연산 ((+,+,--,*) 가능 (예) 섭씨 온도, 지능 지수 |
| 비율 척도 |
절대적 기준값 0 이 존재 하고 연산 ((+,+,--,*,/) 가능 가장 많은 정보 갖는 척도 (예) 무게, 나이, 연간소득, 제품가격, 절대 온도, 농도, 키, 몸무게 등 |
| 기준 | 구분 | 순서 | 구간(간격) | 비율 |
| 명목척도 | O | X | X | X |
| 순서척도 | O | O | X | X |
| 구간척도 | O | O | O | X |
| 비율척도 | O | O | O | O |
[기출문제] 측정 대상이 어느 집단에 속하는지 분류할 때 사용되는 척도로 성별(남, 여) 구분,
출생지(서울특별시, 부산광역시 경기도 등) 구분 등을 할 때 사용되는 척도는 무엇인가?
정답: 명목척도
6. 통계적 분석 방법

① 기술 통계(descriptive statistic)
- 수집된 자료를 정리·요약하기 위해 사용되는 기초통계
- 숫자로 표현하는 방식 : 평균, 표준편차, 중위수, 최빈값, %
- 그림으로 표현하는 방식 : 막대그래프, 원그래프, 꺾은선그래프
- 기술통계 자체로도 여러 용도에 쓰이나 대게 자세한 통계적 분석을 위한 전 단계 역할
② 추론(추측, inferential) 통계
- 모수 추정, 가설 검정(hypothesis test), 회귀 검정, 예측(forecasting)
7. 확률(probability)
(1) 확률
- 특정 사건이 일어날 가능성의 척도
- 표본공간(sample space, Ω) : 나타날 수 있는 모든 결과들의 집합
- 원소(element) : 나타날 수 있는 개개의 결과
- 사건(event) : 표본공간의 부분집합
(2) 조건부 확률(conditional probability)
- 사건 A가 일어났다는 가정 하의 사건 B의 확률
- 사건 A가 주어졌을 때 조건부 확률 = P(B|A)
P(B|A) = P(A∩B) P(A) , P(A)〉0 - 두 사건 A, B가 서로 독립이면, P(A ∩ B) = P(A) • P(B)
- 두 사건 A, B가 서로 독립일 때, 사건 A가 일어났다는 가정 하의 사건 B의 확률
P(B|A) = P(A)•P(B) P(A) , P(A)〉0
[기출문제] P(A)=0.3, P(B)=0.4이다. 두 사건 A와 B가 독립일 경우 P(B|A)는 얼마인가?
정답: P(B|A) = 0.3•0.4 0.3 = 0.4
(3) 분산, 표준편차, 백분위수
① 확률 변수의 흩어진 정도 → 분산과 표준편차, μ는 X의 기댓값
var(X) = E(X − μ) 2
sd(X) = √Var(X)
② 백분위수
P(X ≦ xq) = q/100, 0≦q≦100
8. 확률 변수 및 확률 변수의 종류
(1) 확률 변수(random variable)
- 특정 값이 나타날 가능성이 확률적으로 주어지는 변수
(2) 확률 변수와 확률 분포의 종류
① 이산형 확률 변수(discrete variable)
- 0이 아닌 확률값을 갖는 셀 수 있는 실수 값
(예) 베르누이, 이항분포, 기하분포, 다항분포, 포아송분포 등
- I) 베르누이 분포 : 결과가 2개만 나오는 경우 (예) 동전 던지기
- ii) 이항 분포 : 베르누이 시행을 n번 반복했을 때 k번 성공할 확률
- iii) 포아송 분포 : 시간과 공간 내에서 발생하는 사건의 발생 횟수에 대한 확률분포
② 연속형 확률 변수(continuous variable)
- 특정 실수 구간에서 0이 아닌 확률을 갖는 확률 변수
- 사건의 확률이 확률 밀도함수의 면적으로 표현 (예) 균일분포, 정규분포(z-분포), 지수분포, t-분포, X 2 -분포, F-분포 등
| * 두 집단간의 평균이 동일한지 검정(평균 검정) : t-분포, z-분포 * 두 집단간 분산의 동일성 검정(분산 검정) : F-분포 * 범주형 자료에 대한 두 집단간 동질성 검정 : X 2 -분포 |
(3) 정규 분포(Normal Distribution)
- 특정 값의 출현 비율을 그렸을 때, 중심(평균값)을 기준으로 좌우 대칭 형태로 나타나며, 이것은 종의 모양으로 나타난다.
- 표준 정규분포(Standard normal distribution)는 평균이 0이고 표준편차가 1인 분포이며, z-분포라고 부르기도 한다.

(4) t-분포(t-distribution)
- 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포
- 정규분포보다 퍼져 있고 자유도가 커질수록 정규분포에 가까워진 다. n = 30
- 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용
(5) 중심극한정리
- 표본의 크기가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규 분포에 가까워진다.
9. 점 추정과 구간 추정
* 추정(estimation): 표본으로부터 미지의 모수를 추측하는 것
① 점 추정(point estimation)
- 모수가 특정한 값일 것이라고 추정하는 것
- 사실상 추정이 얼마나 정확한가를 판단하기가 불가능
② 구간 추정(interval estimation)
- 점추정의 정확성을 보완하는 방법
- 일정한 크기의 신뢰수준으로 모수가 특정한 구간에 있을 것이라고 선언하는 것, 구해진 구간 → 신뢰구간
- 일반적인 신뢰구간 : 90%, 95%, 99% 확률 이용
- 신뢰수준 95%의 의미
-- 한 개의 모집단에서 동일한 방법으로 동일한 자료의 개수의 확률표본을 무한히 많이 추출하여 각 확률 표본마다 신뢰
구간을 구하면, 이 무한히 많은 신뢰구간 중에서 95% 신뢰구간이 미지의 모수를 포함한다는 의미
10. 가설 검정
① 가설 검정
- 모집단에 대한 어떤 가설을 설정한 후, 그 가설의 채택 여부 결정하는 방법
② 가설의 종류
I) 귀무가설(H0) : 모수에 대한 가설 중 간단하고 구체적인 표현 설정
ii) 대립가설(H1) : 확실하게 증명하고 싶은 가설, 뚜렷한 증거가 있어야 채택할 수 있는 가설
③ 가설 검정 과정
- 표본 관찰 또는 실험을 통해 귀무가설(H0)과 대립가설(H1) 중에서 하나를 선택하는 과정
④ 가설 검정의 절차
1) 가설의 설정 – 귀무가설(H0), 대립가설(H1)
2) 유의 수준 𝜶 결정 : 보통 0.1, 0.05, 0.01 중 하나 선택
3) 기각역(유의확률) 설정 : 검정 통계량의 분포를 이용하여 기각역 설정
4) 검정 통계량 계산 : 표본으로부터 검정 통계량 계산
5) 가설 채택의 여부 결정 : 검정 통계량과 기각치를 비교하여 귀무가설의 채택여부를 결정
11. 주요 용어
1) p-값(p-value)
- 관측된 검정 통계량의 값보다 대립가설을 지지하는 검정 통계량이 나올 확률
- p-값이 미리 주어진 기준값(0.01, 0.05, 0.1 중 한 개의 값)인 유의수준보다 작으면
⇒ 귀무가설이 나올 가능성이 적다고 판단 ⇒ 귀무가설 기각, 대립가설 채택
- 유의 수준은 보통 0.05를 사용
2) 기각역(critical region, C)
- 귀무가설을 기각하는 통계량의 영역
12. 가설 검정에서의 오류(error)
① 제1종 오류(Type Ⅰ error: α)
- 귀무가설 H0이 옳은데도 H0을 기각하게 되는 오류
② 제2종 오류(Type Ⅱ error: β)
- 귀무가설 H0이 옳지 않은데도 H0을 채택하게 되는 오류
- 두 가지 오류는 서로 상충관계
- 일반적으로 제1종 오류(α)의 크기를 0.01, 0.05, 0.1 등으로 고정시키고, 제2종 오류(β)가 최소가 되도록 기각역을 설정
| 가설검정결과 정확한 사실 | H0이 사실이라고 판정 | H0이 사실이 아니라고 판정 |
| H0이 사실임 | 옳은 결정 | 제1종 오류(α) |
| H0이 사실이 아님 | 제2종 오류(β) | 옳은 결정 |
[기출문제] 아래는 chickwts 데이터프레임을 분석한 것이다. 다음 중 결과에 대한 해석이 잘못된 것은?

① 전체 관측치 수는 70개이다.
② 99% 신뢰구간을 구하기 위해서는 “conf.level=0.99”라는 옵션을 사용할 수 있다.
③ 닭 무게의 점 추정량은 261.3이며, 95% 신뢰구간은 242.8에서 279.8이다.
④ 닭 무게에 대한 p-value는 p-value<2.2e-16이므로 귀무가설이 기각된다.
정답: ①
(풀이)

13. 모집단의 모수에 대한 검정 방법
| 모수적 검정 (parameteric method) | 비모수적 검정 (nonparameteric method) | |
| 가설의 설정 | 가정된 분포의 모수(모평균, 모비율, 모분산)에 대해 가설을 설정 | 가정된 분포가 없으므로, 가설은 단지 ‘분포의 형태가 동일하다’ 또는 ‘분포의 형태가 동일하지 않다’와 같이 분포의 형태에 대해 설정 |
| 가설의 검정 | 관측된 자료(표본평균, 표본분산 등)를 이용해 검정을 실시 | 관측값들의 순위(rank)나 두 관측값의 차이의 부호(sign) 등을 이용해 검정 (예) 부호 검정(sign test), 윌콕슨의 순위합검정(rank sum test), 윌콕슨의 rank test, 만-위트니의 U 검정, 런 검정(run test), 스피어만 순위상관계수 |
2. 기초 통계 분석
1. 기술 통계(description statistic)
- 자료의 특성을 표, 그림, 통계량 등을 사용해 쉽게 파악할 수 있도록 정리/요약하는 것
(1) 통계량에 의한 자료 정리
① 중심 위치 측도 : 표본평균, 중앙값, 최빈값
* 중심 위치의 대푯값을 선정하는 기준
I) 명목 척도로 측정된 데이터 → 최빈값 사용
ii) 분포가 대칭이고 이상값이 존재하지 않으면 → 표본평균 사용
iii) 비대칭이거나 이상값이 존재하면 → 중앙값 사용하고 표본평균은 참고 값으로 비교
iv) 순위 척도로 측정된 데이터 → 중앙값 사용
[예] 10개의 표본 데이터에 대한 중심위치의 척도

② 산포의 측도
- 표본분산, 표본표준편차, 범위, 사분위수범위, 변동계수, 백분위수
③ 분포의 형태에 대한 측도 : 왜도, 첨도
- 왜도 : 분포의 비대칭 정도를 나타내는 측도, 정규분포의 외도 = 0
- 첨도 : 분포의 중심에서 뾰족한 정도를 나타내는 측도, 정규분포의 첨도 = 3

(2) 그래프에 의한 자료 정리
① 범주형 자료 : 막대그래프, 파이차트, 모자이크 플랏 등
② 연속형 자료 : 히스토그램, 줄기-잎 그림, 상자그림, 산점도 등
| 범주형 자료 | 막대 그래프 | 파이 차트 | 모자이크 플랏 |
| 연속형 자료 | 히스토그램 | 줄기-잎 그림 | 상자그림 |
2. 공분산과 상관계수
1) 용어 정의
- 종속변수(반응변수, Y): 다른 변수에 영향을 받는 변수
- 독립변수(설명변수, X): 종속변수에 영향을 주는 변수
- 종속변수와 독립변수의 관계를 산점도 그래프로 표시할 수 있다.
참고) 산점도: 가장 기본이 되는 그래프, x축과 y축으로 구성된 좌표위에 이차원 자료를 점으로 두 변수 간의 관계를 나타내는 데 사용하는 그래프
- 산점도에서 확인해야 할 사항(4가지)
I) 두 변수 사이의 선형(직선) 관계가 성립하는가?
ii) 두 변수 사이의 함수 관계(직선 혹은 곡선)가 성립하는가?
iii) 이상값의 존재하는가?
iv) 몇 개의 집단으로 구분되는가?
2) 공분산(covariance) : cov()
- 공분산은 두 확률 변수가 함께 변하는지를 측정
- 한 변수가 커질 때 다른 변수가 함께 커지거나, 한 변수가 작아질 때 다른 변수가 함께 작아 지는 것과 같이 크기 변화의 방향이 같다면 공분산은 양의 값을 가진다.
- 반대로 한 변수가 커질 때 다른 변수가 작아지거나, 한 변수가 작아질 때 다른 변수가 커지면 공분산은 음의 값을 가진다. - 만약 두 변수의 값이 서로 상관없이 움직인다면 공분산은 0이다.
3) 상관계수(correlation) : cor()
- 두 변수 X 와 Y 간의 선형 상관관계를 계량화한 수치,
- 두 확률변수 X, Y의 공분산을 각 확률변수의 표준 편차의 곱으로 나눈 값
- +1과 -1 사이의 값을 가지며(-1 ≦ r ≦1),
+1은 완벽한 양의 선형 상관 관계,
0은 선형 상관 관계없음,
-1은 완벽한 음의 선형 상관 관계를 의미
4) 상관계수의 종류
① 피어슨 상관계수
- 등간 척도 이상으로 측정되는 두 변수의 상관관계 측정
- 두 변수간의 선형관계의 크기를 측정하는 값으로 비선형적인 상관관계는 나타내지 못함
- (예) 공분산과 상관계수
② 스피어만 상관계수
- 서열 척도인 두 변수의 상관관계 측정하는데 사용
- 비선형 상관관계도 표시
(예) 국어점수와 영어 점수 간의 상관관계 → 피어슨 상관계수
국어성적 석차와 영어 성적 석차의 상관관계 → 스피어만 상관계수
- 피어슨 상관계수와 스피어만 상관계수 비교
| 구분 | 피어슨 상관계수 | 스피어만 상관계수 |
| 개념 | 등간척도 이상으로 측정된 두 변수의 상관관계 측정 | 순서(서열)척도인 두 변수들간의 상관관계 측정 |
| 특징 | 연속형 변수, 정규성 가정 | 순서형 변수, 비모수적 방법 |
| 상관계수 | 피어슨 r(적률상관계수) | 순위상관계수 ρ(로우) |
| R 코드 | cor(x, y, method=c(‘pearson’, ‘spearman’) | |
3. 상관 분석(Correlation Analysis): cor.test()
- 두 변수 간의 관계인 상관계수가 통계적으로 유의한 지를 검정하는 분석
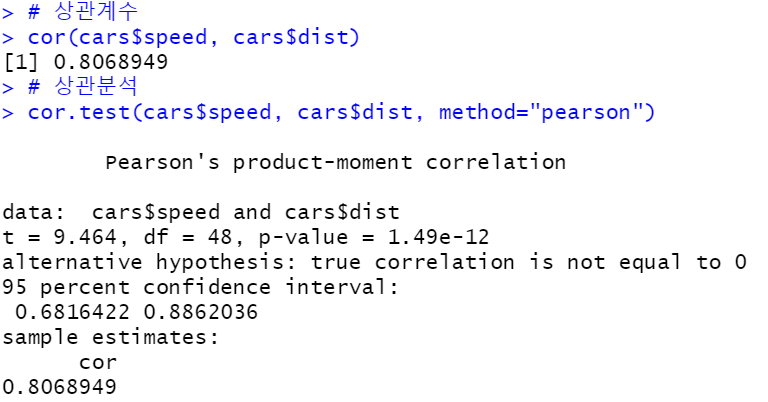
해석) cars 데이터셋에서 speed 변수와 dist 변수 사이의 상관계수는 0.8068949이며, 이 상관계수에 대한 상관분석은 p-value가 1.49e-12이므로 유의수준 0.05에 비해 작으므로 통계적으로 유의한 상관계수이다.
- 상관분석 예제
1) 1단계: 산점도 그려서 두 변수의 상관의 정도를 시각화 해 본다 > plot(drat, disp)

2) 2단계: 상관계수를 구해본다.

3) 3단계: 상관분석을 하여 상관계수의 통계적 유의성을 검정한다.
- Hmisc 패키지의 rcorr() 함수를 이용하면 상관계수와 상관분석을 동시에 진행할 수 있음
3. 회귀 분석
1. 회귀 분석의 개요
1) 회귀 분석의 정의
- 하나 또는 그 이상의 독립변수들이 종속변수에 미치는 영향을 추론하는 통계기법
- 변수의 종류
① 종속변수(반응변수, Y): 영향을 받는 변수, 분석의 대상이 되는 변수
② 독립변수(설명변수, X1, X,2 ,...): 종속변수에 영향을 주는 변수
- 회귀분석 종류: 단순회귀분석과 다중회귀분석
-- 1) 단순회귀분석: 하나의 독립변수가 사용된 회귀 분석
𝒚 = 𝒘𝒙 + 𝒃 w : 계수(가중치), b : 절편(편향)
-- 2) 다중회귀분석: 두개 이상의 독립변수가 사용된 회귀 분석
𝒚 = 𝒘𝟎𝒙𝟎 + 𝒘𝟏𝒙𝟏 + 𝒘𝟐𝒙𝟐 + ⋯ + 𝒘𝒏𝒙𝒏 + 𝒃
- 회귀 계수 추정법 : 최소제곱법
-- 실제 참값과 회귀 모델이 출력한 예측값 사이의 잔차의 제곱의 합을 최소화하는 w(계수)와 b(절편)를 구하는 것이 목적-> Least Square, 최소 제곱법
𝑪𝒐𝒔𝒕𝒕𝒓 = ∑(𝒚𝑰 − 𝒚̂𝒊) 𝟐 𝒊
-- 잔차 제곱의 합이 가장 작은 회귀선을 선택 𝒚̂𝒊 = 𝒃 + 𝒘𝒙𝒊
-- 회귀계수의 추정
- 오차항 𝜺𝒊

>> 회귀 계수의 추정은 오차들의 제곱합을 이용하여 구한다.

- 최소제곱법과 최소제곱추정량
회귀계수추정의 한 방법으로 오차들의 제곱합을 최소로 하는 𝛽0 , 𝛽1의 추정량인 𝑏0 , 𝑏1를 구하는 최소 제곱법을 통해 구한 추정량을 ‘최소제곱추정량’
-- 추정된 회귀직선
- 회귀계수에 대한 추정량 𝑏0, 𝑏1과 종속변수 Y의 예측값을 𝑦̂ 이라 하면, 추정된 회귀직선은 다음과 같다
2) 회귀 분석의 검정
- 회귀식(모형)에 대한 검증: F-검정
- 회귀계수들에 대한 검증: t-검정
- 모형의 설명력은 결정계수(R2 ), 결정계수는 0~1사이의 값
- 단순회귀분석의 결정계수는 상관계수의 제곱과 같음
- 단순회귀에서의 상관계수 = √R2, 부호는 기울기 상관계수와 동일
3) 회귀 모델의 평가 기준: MAE, MSE, RMSE, R2
(1) Residuals(잔차): 실제 값과 예측 값의 차이(오차)

(2) Mean Squared Error(MSE, 평균제곱오차): 잔차를 제곱의 합으로 계산

(3) Root Mean Squared Error(RMSE): MSE에 루트를 씌워 실제 값과 유사한 값으로 변경

(4) 𝑅^2 (결정계수)

- 학습한 회귀 모델이 얼마나 데이터를 잘 표현하는 지에 대한 정도를 나타내는 통계적인 척도
- 0 과 1사이의 값을 갖는다. 1에 가까울수록 회귀모델이 데이터를 잘 표현한다는 것을 의미
(5) Adjusted 𝑅^2 (수정된 결정계수)

- 독립변수 개수가 많아질수록 결정계수의 값이 커지게 되는 것을 보정한 것이 수정된 결정계수
- 표본의 크기와 독립변수의 수를 고려하여 계산하게 되며, 다중회귀분석 경우 사용
2. 단순선형회귀
- 하나의 독립변수가 사용된 선형회귀 분석
- 단순선형 회귀모형
-- 두 확률변수 X, Y에서 X가 독립변수이고, Y가 종속변수일 경우 독립변수 X의 개별값 𝑥1 , 𝑥2, … , 𝑥𝑛 에 대응하는 종속
변수 Y의 관찰값 𝑦1 , 𝑦2, … , 𝑦𝑛 에 대해 다음과 같은 모형을 단순선형회귀모형이라고 합니다.

- 회귀계수
- 위의 식에서 두 상수 𝛽0 , 𝛽1을 (모집단)회귀계수라 하는데, 이는 각각 직선의 방정식에서 절편과 기울기의 역할을 합니다.
- 두 상수는 미지의 모수로, 표본으로부터 추정을 통해 구합니다.
- 추정된 회귀계수를 이용하여 구한 식으로 나타나는 직선 > ‘추정된 회귀직선’
[기출문제] 아래는 자동차의 속도(speed)와 제동거리(dist)의 관계를 분석한 회귀분석 결과이다. 회귀분석 35 의 가정이 모두 만족되었다고 할 때, 10mile 속도로 달리고 있는 자동차의 제동거리를 예측하시오.

(풀이)

[기출문제] 아래는 기대수명(Life.Exp)과 문맹률(illiteracy)와의 관계를 나타내는 회귀분석 결과이다. 이를 사용하여 계산한 기대수명과 문맹률 간의 피어슨 상관계수로 적절한 것은?

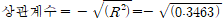
(풀이) 선형회귀분석 상관계수는 결정계수에 제곱근(root)를 씌운 값과 같으며, 부호는 기울기의 부호를 따른다.
3. 다중회귀분석(중회귀분석)
1) 다중선형회귀분석
- 두개 이상의 독립변수가 사용된 선형회귀 분석
- 여러 독립 변수가 +로 연결해 나열하여 다중선형 회귀모델 만듦
- lm() 함수로 중선형 회귀를 진행한 후 summary()로 결과 확인
- summary()의 결과를 읽는 방법은 선형 회귀와 동일
- F-통계량 해석에는 차이가 있음
-- 단순선형 회귀 귀무가설 : ‘H0 : β1 = 0이다.’
-- 다중선형회귀 귀무가설 : ‘H0 : 모든 계수가 0이다.’’ (β0=β1=β2=...βp=0)
=> p-value < 0.05이면 하나 이상의 설명 변수의 계수가 0이 아니다.
-- 다중회귀모형

-- 회귀계수

-- 오차항

- 다중선형회귀분석의 예
2) 다중선형회귀분석의 다중공선성
- 다중회귀분석에서 설명변수들 사이에 선형 관계가 존재하면 회귀계수의 정확한 추정이 곤란해짐
3) 다중공선성의 검사
- 분산팽창요인(VIF) : 10보다 크면 다중공선성이 있는 것으로 간주
- 10이상이면 문제가 있다고 보고, 30보다 크면 심각, 선형관계가 강한 변수는 제거
4. 선형회귀 모형의 유의성 검정
① 모형(회귀식)이 통계적으로 유의미한가?
- F 통계량 확인, 유의수준 5% 하에서 F 통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유 의
② 회귀계수들이 유의미한가?
- 해당 계수의 t통계량과 p-값 또는 이들의 신뢰구간을 확인한다.(p-값이 0.05 보다 작으면 회귀계수 유의)
③ 모형이 얼마나 설득력을 갖는가?
- 결정계수(R 2 )를 확인한다. 결정계수가 0에서 1사이의 값을 가지며, 높은 값일수록 추정된 회귀식의 설명력이 높다.
5. 선형회귀분석의 가정(5가지)
I) 선형성(독립변수의 변화에 따라 종속변수도 일정크기로 변환)
ii) 독립성(잔차와 독립변수의 값이 관련되어 있지 않음)
iii) 등분산성(독립변수의 모든 값에 대해 오차들의 분산이 일정)
iv) 비상관성(관측치들의 잔차들끼리 상관이 없어야 함)
v) 정상성(잔차항이 정규분포를 이루어야 함) → 정규분포 확인 : Q-Q Plot, Shapiro-Wilk 검정
6. 잔차 그래프로 살펴본 선형회귀분석의 가정 → 잔차 분석
A) 잔차가 특별한 형태가 없이 무작위로 퍼져 있기 때문에 아주 좋은 잔차 그래프라고 할 수 있다.
B) 잔차들이 뭉쳐 세트(set)를 이루고 있기 때문에 독립성 가정에 위배되는 것으로 보인다.
C) 잔차 형태가 U자를 띄고 있기 때문에 선형성 가정에 위배되는 것으로 보인다.
→ 2차항의 설명변수가 필요함
D) 잔차의 분포가 점점 커지고 있기 때문에 등분산성 가정에 위배되는 것으로 보인다.
E) 잔차의 분포가 X값이 커짐에 따라 잔차가 커지는 모습을 보여 잔차와 입력변수간에 아무런 관련성이 없다고 보기힘듦 → 새로운 설명변수가 필요함
7. 정상성(정규성) 검정
- 샤피로-윌크 검정(Shapiro-Wilk test)이나 Q-Q plot으로 확인
1) 정규성 검정
- 데이터 셋의 분포가 정규분포(Normal Distribution)을 따르는 지를 검정하는 것
- 통계적인 여러 검정법들이 데이터의 정규분포를 가정하고 수행되기 때문에 데이터 자체의 정규성을 확인하는 검정 과정이 필수적
2) 정규성 검정 종류
① 샤피로-윌크 검정(Shapiro-Wilk test)
② Q-Q plot(Quantile-Quantile plot)
3) 정규성 검정의 가설
- H0(귀무가설) : 데이터셋이 정규분포를 따른다.
- H1(대립가설) : 데이터셋이 정규분포를 따르지 않는다.
4) 정규성 검정 예제
bmi가 정규분포를 따르는지 확인
1) 샤피로-윌크 검정(Shapiro-Wilk test)
shapiro.test(bmi)
# shapiro-Wilk normality test
#
# data: bmi
# W = 0.99104, p-value = 0.2523
# 해석) p-value가 0.2523으로 0.05보다 큰 값
# 귀무가설 기각이 안되므로 bmi는 정규분포를 따른다고 할 수 있다.
2) Q-Q plot qqnorm(bmi) qqline(bmi)
- 해석) QQ plot의 점들이 기울기의 직선상에 놓이면 자료가 해당 분포를 잘 따른다고 할 수 있다.
- 데이터셋의 점들이 라인을 따라서 잘 붙어있으므로 정규성을 따른다고 할 수 있다.
8. 최적회귀방정식 - 설명 변수의 선택법
→ 가능한 범위 내에서 적은 수의 설명변수 포함
1) 단계적 변수 선택(Stepwise Variable Selection) : 변수의 선택기준 → AIC가 낮은 것부터 선택
- AIC(Akaike information cirterion) : 모델의 상대적 품질 평가 척도
① 전진 선택법(forward selection)
- 절편만 있는 상수 모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
- 제곱합의 기준으로 가장 설명을 잘하는 변수를 고려하여 그 변수가 유의하면 추가, 그렇지 않으면 추가 멈춤
② 후진 제거법(backward elimination)
- 독립변수 후보 모두를 포함한 모형에서 출발해 제곱합의 기준으로 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더이상 유의하지 않은 변수가 없을 때까지 설명변수를 제거하고 이 때의 모형을 선택
③ 단계별 방법(stepwise method) = 전진선택법 + 후진 제거법
- 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존변수가 그 중요도가 약화되면 해당변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 필요 없을 때 중단.
2) 단계적 변수 선택법의 step() 함수
형식 : step(lm(종속변수~설명변수, 데이터세트),
scope=list(lower=~1,upper=~설명변수), direction=" 변수선택방법“)
① 전진선택법
step(lm(Pemax~1, Bio), scope=list(lower=~1, upper=나이+키+체중+BMP+RV+FRC+TCL), direction="forward")
② 후진제거법
step(lm(Pemax~나이+키+체중+BMP+RV+FRC+TCL, direction="backward")
③ 단계별방법
step(lm(Pemax ~1, Bio), scope=list(lower=~1, upper=나이+키+체중+BMP+RV+FRC+TCL), direction="both") 41
[기출문제] 아래는 1888년 스위스의 47개 지역의 출산율 자료를 사용해 회귀분석을 실시한 결과이다. 최 적화회귀방정식을 선택하기 위해 후진제거법(backward elimination)으로 설명변수를 선택하려고 한 다. 이때 가장 먼저 제거되어야 하는 설명변수는 무엇인가?
<아래>
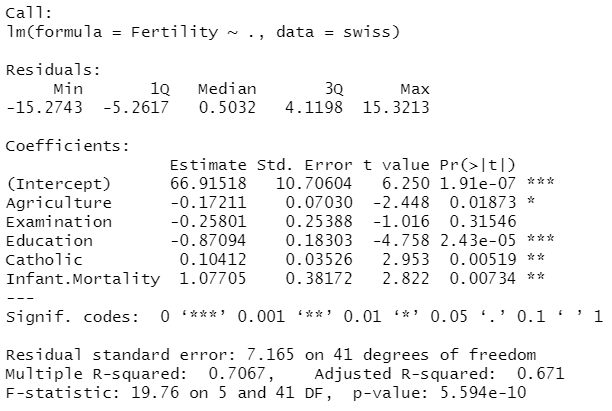
① Agriculture
② Examination
③ Education
④ Catholic
정답: ②
4. 시계열 분석
1. 시계열 자료
- 시계열 자료(Time-series Data) : 시간의 흐름에 따라 관측된 데이터
2. 정상성(Stationary)
- 시점에 상관없이 시계열이 특성이 일정하다는 것을 의미하며 아래의 조건을 만족해야 함
① 평균이 일정(모든 시점에서 일정한 평균을 가짐)
② 분산도 일정
③ 공분산은 단지 시차에만 의존, 시점 의존하지 않는다.
- 비정상 시계열을 정상 시계열 바꾸는 방법
① 추세를 보이는 경우(평균이 일정하지 않은) → 차분(difference)을 통해 정상화
② 시간에 따라 분산이 일정하지 않은 경우 → 변환(transformation)을 통해 정상화
- 차분
① 일반 차분 = 현시점의 자료값 - 전 시점의 자료값
② 계절 차분(Seasonal Difference)
- 현재 시점에서 여러 시점 전의 자료를 빼는 것
→ 계절성을 갖는 비정상 시계열을 정상 시계열로 바꿀 때 계절 차분을 사용
3. 시계열 모형(4가지)
- AR, MA, ARIMA, 분해시계열
1) 자기회귀 모형(Autoregressive model, AR 모형)
- 현 시점 자료가 p 시점 전의 유한개의 과거자료로 설명될 수 있다는 의미, AR(p) 모형
Zt = ϕ1Zt−1 + ϕ2Zt−2+. . . +ϕpZt−p + αt
Zt : 현재 시점의 시계열 자료
Zt−1 , Zt−2 , . . . , Zt−p : 1 ~ p 시점 이전의 시계열 자료
ϕp : p 시점이 현재 시점에 어느 정도 영향을 주는지 나타내는 모수
αt : 백색잡음과정(White noise process, 대표적 정상 시계열), 시계열 분석에서 오차항을 의미
2) 이동평균모형(MA 모형)
Zt = αt − θ1αt−1 − θ2αt−2−. . .−θpαt−p - 이동평균모형(Moving Average model)
- 이동평균모형은 현 시점의 자료를 유한개의 백색잡음의 선형 결합으로 표현되었기 때문에
→ 항상 정상성을 만족
→ 이동평균모형은 장상성 가정이 필요 없다.
3) 자기회귀누적이동평균모형(ARIMA 모형)
- 대부분의 많은 시계열 자료가 자기회귀누적이동평균모형을 따름
- ARIMA 모형은 기본적으로 비정상 시계열 모형
→ 차분이나 변환을 통해 AR 모형이나 MA 모형, ARMA 모형으로 정상화할 수 있다.
- ARIMA(p,d,q) 모형
- p, d, q의 값에 따라 모형의 이름이 다르게 된다.
- p: AR 모형과 관련
- q: MA 모형과 관련
- d: ARIMA에서 ARMA로 정상화할 때 몇 번 차분을 했는지를 의미
- d=0이면 → ARMA(p,q) 모형이라 부르고, 정상성을 만족.
- p=0이면 → IMA(d,q) 모형이라고 부르고, d번 차분 → MA(q)
- q=0이면 → ARI(p,d) 모형이며, d번 차분한 시계열 모형 → AR(p) 모형
(예) ARIMA(0,1,1)
- 1차분 후 MA(1) 활용 ARIMA(1,1,0)
- 1차분 후 AR(1) 활용 ARIMA(1,1,2)
- 1차분 후 AR(1), MA(2), ARMA(1,2) 선택 활용 -> 이런 경우 가장 간단한 모형을 선택하거나 AIC를 적용하여 가장
낮은 모형을 선정
4) 분해 시계열
- 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법, 회귀분석 적인 방법을 주로 사용
- 분해 시계열 구성 요소(4)
I) 추세 요인(trend factor) : 자료가 특정한 형태를 취할 때 추세 요인이 있다고 한다.(선형적, 이차식, 지수형태)
ii) 계절 요인(seasonal factor) : 고정된 주기에 따라 자료가 변화하는 경우(요일,월,사분기자료에서 분기변화)
iii) 순환 요인(cyclical factor) : 알려지지 않은 주기를 가지고 변화하는 자료
iv) 불규칙 요인(irregular factor) : 위의 3가지 요인으로 설명할 수 없는 회귀분석에서 오차에 해당하는 요인
시계열 분석 예제)
5. 다차원 척도법
1. 다차원 척도법(Multidimensional Scaling, MDS)
1) 정의
- 군집분석과 같이 개체들을 대상으로 변수들을 측정한 후 개체들 사이의 유사성/비유사성을 측정하여 개체들을 2차원 또는 3차원 공간상에서 점으로 표현하는 분석 방법
- 목적 : 개체들의 비유사성을 이용하여 2차원 공간상에 점으로 표시하고 개체들 사이의 집단화를 시각적으로 표현, 데이터의 축소의 목적으로 다차원척도법 사용
2) 방법
- 개체들의 거리 계산은 유클리드 거리행렬을 이용
6. 주성분 분석(PCA)
1. 주성분 분석(PCA)
1) 정의
- 상관관계가 있는 변수들을 결합해 상관관계가 없는 변수로 분산을 극대화하는 변수로, 선형결합으로 변수를 축약, 축소하는 기법
- 보통 3개 이내의 변수로 축약하고 이로 인한 정보 손실은 20% 정도로 함
- 목적
- 여러 변수들을 소수의 주성분으로 축소하여 데이터를 쉽게 이해하고 관리
- 주성분분석을 통해 차원을 축소하여 군집분석에서 군집화 결과와 연산속도 개선, 회귀분석에서 다중공선성의 최소화
2) 주성분의 선택법
- 누적기여율(cumulative proportion)이 85%이상이면 주성분의 수로 결정할 수 있음
- scree plot에서 고유값(eigen value)이 수평을 유지하기 전 단계로 주성분의 수를 선택
(예제) 주성분분석(PCA)
> data("USArrests")
# USArressts 데이터셋: 1973년 미국 주별 강력 범죄율 데이터셋
# 주성분분석 > US.prin <- princomp(USArrests, cor= TRUE)
> screeplot(US.prin, npcs=4, type="lines")
# scree plot에서 기울기가 급격하게 변하는 구간을 기점으로 주성분의 수를 결정
[기출문제] 아래는 주성분 분석을 수행한 결과이다. 첫 번째 분산은 전체 분산의 몇 %를 설명하고 있는가?
<아래>
| Comp.1 | Comp.2 | Comp.3 | |
| Standard deviation | 1.5574873 | 0.9943214 | 0.5943221 |
| Proportion of Variance | 0.5748331 | 0.2321003 | 0.1834561 |
| Cumulative Proportion | 0.5748331 | 0.8069334 | 0.9903895 |
정답: 57.4%
'Study > ADsP' 카테고리의 다른 글
| [ADsP 정리] 3. 데이터 분석(4) (1) | 2024.05.20 |
|---|---|
| [ADsP 정리] 3. 데이터 분석(2) (2) | 2024.05.14 |
| [ADsP 정리] 3. 데이터 분석(1) (0) | 2024.05.13 |
| [ADsP 정리] 2. 데이터 분석기획(2) (1) | 2024.05.09 |
| [ADsP 정리] 2. 데이터분석 기획 (0) | 2024.05.06 |
